Science
The Analysis and Geometry of Information

Imagine life without computers, cell phones, TVs, radios, computers, MRI scans, EKG and EEG scans, or GPS systems. All of these required a tremendous amount of mathematics in their development. Stephen Casey, chair and professor of mathematics in the American University Department of Mathematics and Statistics is taking things a step further by looking at the fundamental structures along which information is gathered, stored, and communicated. His research involves tools from many areas of mathematics, including Harmonic and Complex Analysis and Integral and Differential Geometry. Casey recently solved a set of problems involving the structure and communication of information. For this he has published numerous papers, given several invited talks, and been awarded four US government grants, two provisional US patents, a full patent, and one patent pending.
Cell Phone Architectures
In September 2016, Casey was awarded US Patent Number 9,454,511 B2, Windowing methods and systems for use in time-frequency analysis, for his work with friend and colleague Brian Sadler, an electrical engineer and a Fellow of the IEEE. The patent develops a new approach to signal sampling, designed to deal with Ultra-Wide Band (UWB) and Adaptive Frequency Band (AFB) communication systems. These systems require either very high sampling or rapidly changing sampling rates. Casey approached this problem from a signal processing perspective, implementing an appropriate signal decomposition in the analog portion, providing parallel outputs for integrated digital conversion and processing. A second patent, under review, also develops the method with a modified Gegenbauer system designed specifically for UWB signals—US Patent Application 15/274450, Continuation-in-part of 13/464843.
The overarching goal of the theory developed in this patent was to develop a computable atomic decomposition of time-frequency space. The idea was to come up with a way of non-uniformly tiling time and frequency to use the energy of the processing more efficiently. Computability is key. Casey worked with Sadler. These systems are designed so that they can be implemented in circuitry. If the signal has a burst of high-frequency information, the system adaptively tiles quickly and efficiently in time and broadly in frequency, whereas if the signal has a relatively low-frequency segment, it tiles broadly in time and thus energy efficiently in frequency.
Casey says, “The idea is to take advantage of the duality of the time evolution and frequency evolution of information simultaneously. By playing the energy required, if the signal has a burst of high-frequency information, we adaptively tile quickly and efficiently in time and broadly in frequency, whereas if the signal has a relatively low-frequency segment, we can tile broadly in time and thus energy efficiently in frequency.” Experiments show that it makes the communication part of cell phones up to four times more efficient, and thus, one has to charge their phone less frequently.
He adds that “The Gegenbauer functions used in the second patent are really amazing. They cut down any residual ringing from the segmentation problem to a minimum, and make the delivery of the signal really crisp.”
Non-Euclidean Geometry and the Internet
Casey is also working on how to understand the flow of information through the internet. The internet has become central to the daily lives of most businesses, schools, and people. A goal of network security is to keep traffic moving and keep the network free of viruses. The field of network tomography allows the creation of a system that will detect viruses as early as possible and work simply on the geometry or structure of the network itself. Casey has developed a computationally efficient method to monitor internet traffic. His model monitors specific connected subsets of arbitrary weighted graphs (regions of interest) from the input output map corresponding to paths that have crossed such regions. Using this model, one can identify congested areas or even anticipate areas that will get congested, which would allow a system manager to take measures to avoid the stoppage of traffic. Viruses are detected by observing a rapid increase in network activity. He has accomplished his work by developing Harmonic Analysis in settings of both Euclidean and non-Euclidean spaces, and then applying this analysis to two specific problems: signal sampling and network tomography.
Casey says, “This work is part of a more ambitious research project. The idea is to view information geometrically, and then apply the tools of geometry to analyze, communicate and/or store, and reconstruct information.” He was invited to give a sequence of lectures this summer in Austria. One of these involved spherical geometry, and he was invited to tour the Spherical Acoustic Array at the Austrian Academy of Sciences Acoustics Research Institute.
So, what does a non-Euclidean geometry look like? A distinguishing feature of all geometries is what forms the shortest distance between two points, called a geodesic, and how those geodesics intersect. In “flat” or Euclidean geometry, straight lines are the geodesics, two parallel lines will never meet, and all triangles will have interior angles summing to 180 (Pi) degrees. On a sphere, geodesics appear curved (the equator is an example), two parallel geodesics will meet twice antipodally (think north and south poles), and triangles will be “chubby,” with sides curving outwards and angles summing greater than 180 (Pi) degrees all the way to 360 (2 Pi) degrees.
Hyperbolic space requires some pictures. The artist M. C. Escher gave us some insights.

Figure 1 shows the hyperbolic unit disc. One can see an interlocking mesh of angels and demons, infinity spreading out to the “infinity horizon” at the unit circle. The outer figures look smaller, but in hyperbolic geometry, they are all the same size. We can see this if we have our “hyperbolic glasses” on. Casey uses the tools of Complex Analysis and Differential Geometry to work in this geometry.

Figure 2 replaces the angels and demons with triangles. In this geometry, geodesics are smooth arcs meeting the infinity horizon perpendicularly, infinitely many parallel geodesics can meet, and triangles are “skinny,” with sides curving inwards and angles summing from 0 degrees all the way up to but not including 180 (Pi) degrees. These skinny triangles are a key signature of hyperbolic space.
Note an important fact: in both pictures of the hyperbolic disc, we are fitting an infinite amount of information in a finite space!!
Casey works the tools of Harmonic Analysis in non-Euclidean geometries, allowing him to think about information in a manner similar to the cell phone architectures.
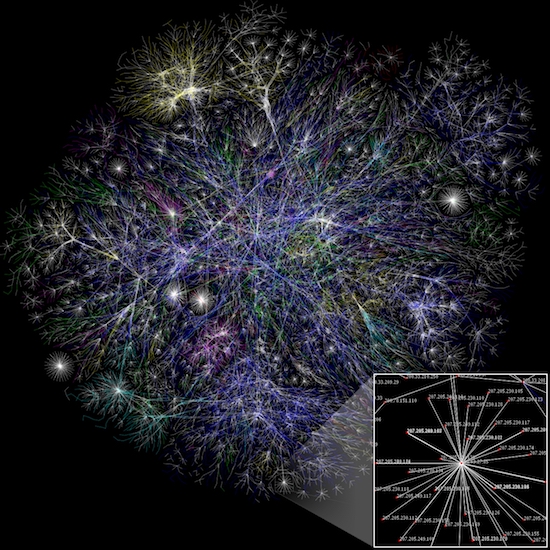
Figure 3 is a picture of the Internet. Several characteristics indicate that its structure can be described using hyperbolic geometry. Information sent through the internet flows inward, from your computer to your server to a larger server to a centralized server and then outward. Trace the paths connecting any three nodes on the picture above, and you will see a signature of hyperbolic space: the skinny triangle. Moreover, the Internet must fit an infinite amount of information in a finite space: there are potentially infinitely many cute cat videos, and people have to share them. We would run out of space if the geometry was not hyperbolic.
Luckily, we won’t. The research has shown that the internet has a hyperbolic structure, allowing Casey to use all his non-Euclidean Harmonic Analysis to study the internet. Very deep work of Casey’s mentor Carlos Berenstein on network tomography gives that the network monitoring can be associated to a problem similar to electrical impedance tomography (EIT) on graphs. It is also associated to the Radon transform on trees. From this work, we develop a strategy to determine the traffic along internet paths.
The natural tool to use in this context is the Radon Transform. In hyperbolic space, we define the Radon Transform of an object by “smoothly adding up” (integrating) over each geodesic that intersects the object. (Think “x-rays.”) Sigurdur Helgason, emeritus professor of mathematics at Massachusetts Institute of Technology, has shown that the Radon Transform uniquely preserves infor-mation in the hyperbolic setting, which then makes it the tool of choice when working in that geometry.
The key ingredient is the attempt to understand what happens in a network from “boundary measurements,” that is, to determine whether all of the nodes and routers are working or not and also measure congestion in the links between nodes by means of introducing test packets in the “external” nodes, the routers. To understand the boundary measurements, we must look at a special mapping—the Neumann-to-Dirichlet map. We must decompose and understand how this map will allow us to reduce the network to a system of linear equations. With this method, we can compute the actual traffic weights from the knowledge of the Dirichlet data for convenient choices of the input Neumann data in a way similar to that done for lattices. In the context of electrical networks, this map takes currents on the boundary and gives voltages on the boundary, and is represented by a matrix. Looking at the internet as modeled as a hyperbolic graph allows for the natural use of the Neumann-to-Dirichlet map, and thus the discrete Radon Transform. The inverse of the discrete Radon Transform completes the problem with its result giving the interior data.
It’s as easy as (a skinny triangle in hyperbolic space, whose internal angles can sum up to but not equal to) Pi.
The Geometry of the Brain
Neuroscientists have observed similarities between the structure of the brain and that of the Internet. As Larry Swanson of the University of Southern California describes, “the Internet has countless local area networks that then connect with larger, regional networks and ultimately with the backbone of the Internet. The brain operates in a similar way. The cerebral cortex is like a mini-Internet.”
Well, not so “mini.” Researchers recently discovered that, unlike a classical computer, which codes information as 0s and 1s, a brain cell uses 26 different ways to code its “bits.” They calculated that the brain could store one petabyte (or a quadrillion bytes) of information.
So, we can fit lots of cute cat videos in our heads, and Casey has a new network to study this fall.
