When the COVID-19 pandemic struck this spring and classes moved online, Senior Professorial Lecturer of Mathematics and Statistics Mike Limarzi spotted a once-in-a-lifetime teaching opportunity. He would teach his students how pandemic models work, using a simplified version of what epidemiologists are currently using to predict the spread of COVID-19.

Limarzi immediately changed course in MATH 125: The Math Workshop. “In the first half of the semester, we analyzed real world problems using modeling, especially linear and exponential models,” he explains. “We had always intended to pivot in the second half of the course to point out some weaknesses in relying solely on these models and how to make adjustments when needed. Because of the coronavirus, we decided to use pandemic modeling to demonstrate how exponential models might work in the short term, but give wildly unhelpful information over time, which is not ideal when trying to stop the spread of a deadly virus.”

Limarzi was also thinking about how students were feeling at the time. “Given that the coronavirus became omnipresent in our lives, we felt that tackling this topic would not only be a valuable mathematical lesson, but it might also help ease some of the students' fears about the outbreak by understanding how diseases traditionally spread,” he says.

Flattening the Curve

For Limarzi, studying the pandemic models was a natural change of course for the class, which focuses on solving real-life problems that involve logical reasoning and quantitative information.

In the course, students are given a problem and must scrutinize whether the problem makes sense, consider how to reliably get the answer (such as using the internet or plugging parameters into a formula), and learn what to do if the problem is unfamiliar enough that no specific solution strategies are apparent. Traditionally, the curriculum stresses problems around real-life issues like compound interest and mortgages, as applications that involve linear and exponential mathematical models.

This spring, Limarzi asked students to come up with reasons why, despite the repeated use of the term "exponential growth" by media outlets, the spread of the coronavirus will not be exponential in the long run. Then the students were tasked with using a realistic model to help understand how the disease might spread.  

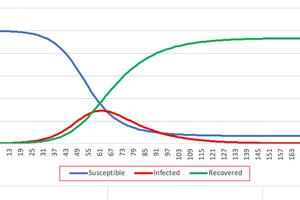
“We chose the SIR Model, which stands for Susceptible-Infected-Recovered, since it is the simplest model, but still insightful,” Limarzi explains. “Based on a few assumptions about the likelihood of new infections in a day and the length of time it takes to recover after having been infected, we had students predict how many new people would be infected in a day, and how many new people will recover from the disease. Then, using Excel, we were able to do this for many days, which then gave us an understanding of how a disease could spread. By adjusting some of the parameters, we could see what "flattening the curve" would actually look like.”

A “Masterpiece” Exam

Limarzi designed what Professor of Mathematics and Statistics Jeff Adler described as a “masterpiece” online final exam for students. “It was sequence of problems that tell a coherent story about lock-down activities, and it touched on every mathematical topic covered in the course: linear growth, exponential growth, value of annuities, modeling of epidemics, Galileo’s square-cube law, group preferences, and most importantly, steps for addressing a problem that’s unlike anything seen before,” Adler says.

The goal was to tell was to tell a story about what students’ lives might be like during self-isolation and show how math plays a role in these everyday experiences, Limarzi says. The exam started with a mayor issuing a stay-at-home order, with the student then finding ways to occupy their time while stuck at home, such as reading a book, baking, posting pictures on Instagram, exercising, or making masks.  

“The math questions related to each of these activities in a natural way,” Limarzi explains. “Here are a few examples: If you make your pancakes half as wide, how many more pancakes could you make? If you invest your money earned from selling masks each week, how much will you have in two months? If you follow a particular work-out regimen, how long will it take you to complete 1,000 sit-ups?”  

Math is Collaborative

Adler points out that the pivot to pandemic modeling required faculty members to develop new materials from scratch at short notice. “Had I been teaching this class on my own, I would have survived by adding a huge additional time investment, cutting corners, and muddling through somehow,” he says. “But with Limarzi’s help, I never had to pull an all-nighter, and I was able to offer what I think was a valuable service to those of our students who are hardest to reach. The experience reminded me of the main perk of academia: the opportunity to work alongside people who are creative, energetic, and conscientious.”

Limarzi says that professors encourage their students to work together during class, so it is only fitting that the professors themselves embrace collaboration as well. “When people think about someone ‘doing math,’ too often they envision a man in his attic at midnight, scribbling furiously by candlelight at his desk, alone.” he says.

“But in reality, math is a collaborative experience. You have an idea that gives someone else a better idea that gives you a great idea. It can be messy, with wrong turns or missteps, but each of these errors gives us insight and guides us to the answer. While preparing these lectures, we embraced the process: drafts, rewrites, rearranging, and sometimes scrapping it all and starting over again. But each professor provided valuable feedback that helped to make the lectures more thought-provoking, more engaging, more memorable for our students.”